画多边形

正多边形

用 canvas 画一个边长为 size 的正 n 边形。

以正六边形为例，如下图所示，正六边形的每个角都在圆上面，我们就可以利用三角函数把各个顶点的坐标求出来，然后每个坐标点相连即可。

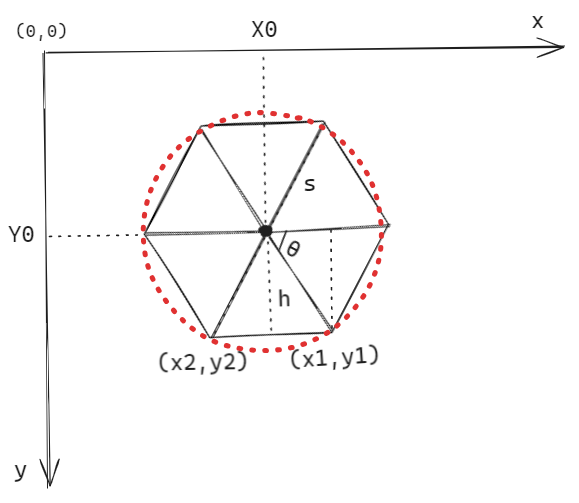
已知：

1. 圆心到各个角的长度相同；
2. θ = 360° / 6；
3. Π = 180° 2Π = 360°；

那么我们就能求出：

x1 = s * cos(60°) + X0
y1 = s * sin(60°) + Y0

x2 = s * cos(120°) + X0
y2 = s * sin(120°) + Y0

...
Xn = s * cos(nθ) + X0
Yn = s * sin(nθ) + Y0

可以理解为我们在画一个圆，不过只在这个圆形边上取了（或者说采样）六个点，然后把这个六个点连接起来。

function drawPolygon(
    ctx: CanvasRenderingContext2D,
    /** n 边形 */
    n: number,
    dx: number,
    dy: number,
    /** 圆心到角的距离 */
    size: number,
) {
    // 2PI = 360°，求出单个角度对应的弧度
    const degree = (2 * Math.PI) / n;
    // 开始画图
    ctx.beginPath();

    // 圆形的整个角度是 360°，开始画圆（在0-360区间）
    for (let i = 0; i < n; i++) {
        const x = Math.cos(i * degree);
        const y = Math.sin(i * degree);

        ctx.lineTo(x * size + dx, y * size + dy);
    }

    ctx.closePath();
}

边数量：  内圆半径：1020304050  外圆半径：1020304050

画一个五角星

两个正五边形顶点相连的结果可以是一个五角星。如下午所示，最外层的正五边形的顶点与最内侧的正五边形顶点两连就可以得到五角星的一条边， 而这条边与圆心到正五边形顶点的边围成的夹角θ就等于：360°/5/2。在绘制两个正五边形时角度错开θ°。

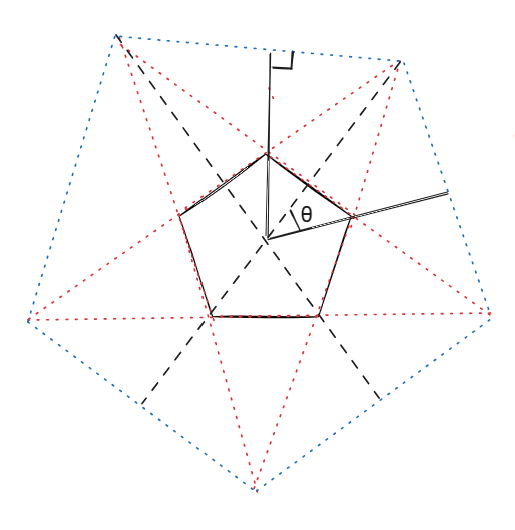
对应代码如下：

function drawStar(
    ctx: CanvasRenderingContext2D,
    /** n 角星 */
    n: number,
    dx: number,
    dy: number,
    /** 内正 N 边形到圆心的距离 */
    size: number,
    /** 外正 N 边形到圆心的距离 */
    externalSize = size * 2,
) {

    // 正 n 边形对应夹角
    const degree = (2 * Math.PI) / n;
    // 要错开的角度
    const halfDegree = degree / 2;

    ctx.beginPath();

    // 因为要绘制两个正 n 边形，因此要 *2，
    // 每次循环直接求出两个 n 边形对应的坐标
    // +=2 是为了确保角度计算不出错，
    // 比如 六边形的 halfDegree=30°，但每个角需要间隔 60° 才能画出正六边形
    for (let i = 0; i < n * 2; i += 2) {
        const x1 = Math.cos(i * halfDegree);
        const y1 = Math.sin(i * halfDegree);

        const x2 = Math.cos((i + 1) * halfDegree);
        const y2 = Math.sin((i + 1) * halfDegree);

        ctx.lineTo(x1 * size + dx, y1 * size + dy);
        ctx.lineTo(x2 * externalSize + dx, y2 * externalSize + dy);
    }

    ctx.closePath();
}

上面代码不仅适应于画五角星，可以支持n角星。