计算器实现原理

要实现一个计算器的功能，通常的思路是：

1. 等待用户输入完成，比如输入了 2*(4+2)/6；
2. 根据输入的内容计算出结果；

使用 eval 函数可以轻易的计算出结果，如果不使用 eval 函数，又该怎么实现呢？

eval(expression);

中缀表达式和后缀表达式

上面的表达式——2*(4+2)/6 被称为中缀表达式，是一个通用的算术或逻辑公式表示方法，操作符处于操作数的中间，中缀表达式是人们常用的算术表示方法。

但是中缀表达式却不容易被计算机解析。中缀表达式中由于运算符优先级而需要进行中间步骤（比如乘除比加减优先级高，而小括号优先级更高），但计算机更擅长顺序执行；

后缀表达式也称为逆波兰式，逆波兰式对于计算机是比较简单易懂的结构，但对人类的思维结构来说却不容易理解。

2*(4+2)/6 写成逆波兰式则是：242+*6/。

逆波兰式求值过程

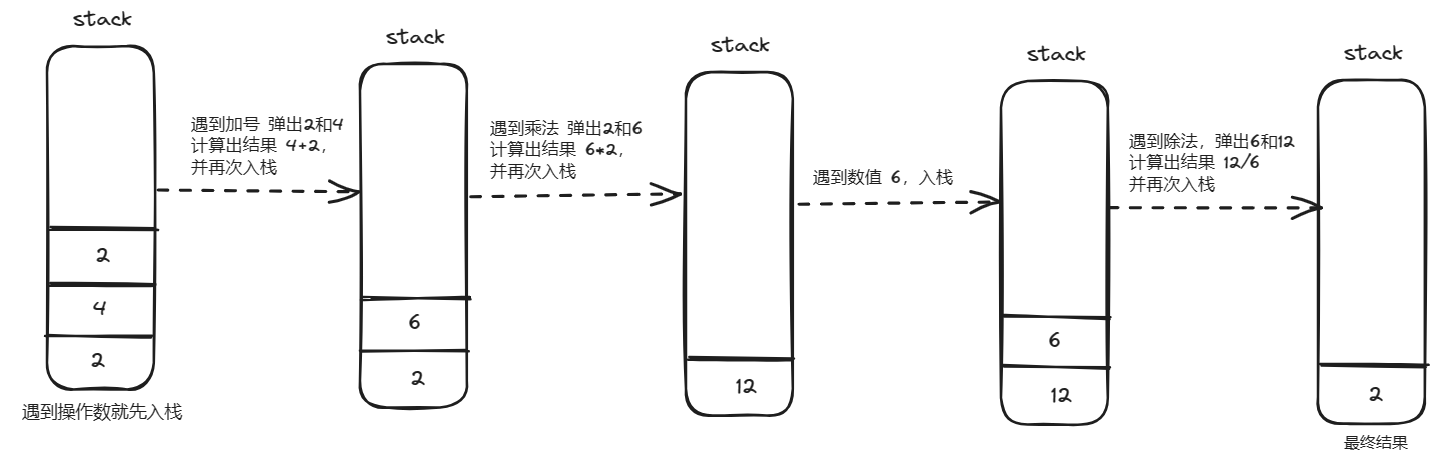
242+*6/ 表达式求值的过程如下：

1. 从左到右扫描字符串，把操作数压入栈中；
2. 如果遇到操作符，则弹出栈中前两个操作数进行运算；
3. 把上一步的运算结果再次压入栈中；
4. 重复 2-3 的步骤，直到表达式遍历完，这时候栈里会只剩下一个操作数，这个操作数就是最终的运算结果；

核心代码：

const isNumber = (char: string) => {
    const charCode = char.charCodeAt(0);
    return charCode > 47 && charCode < 58;
}

function calcReversePolishNotation(expression: string) {
    const stack: string[] = [];

    /** 遍历表达式 */
    for (let char of expression) {

        /** 是不是数字，是的话就入栈 */
        if (isNumber(char)) {
            stack.push(char);
            continue;
        }

        /** 是操作符的情况就计算结果，然后把结果再入栈 */
        const newVal = `${calc(char)}`;
        /** 把新的值再次压入栈中 */
        stack.push(newVal);
    }

    /** 把最后的计算结果弹出即可 */
    return stack.pop();
}

// test: 2*(4+2)/3
const result = calcReversePolishNotation('242+*3/');
console.log(result);    // 4

上面代码中，计算 newVal 的主要的流程是：弹出两个栈顶成员，根据操作符做相应运算。代码如下：

const calcMap = {
    '+': (num1: number, num2: number) => num1 + num2,
    '-': (num1: number, num2: number) => num1 - num2,
    '*': (num1: number, num2: number) => num1 * num2,
    '/': (num1: number, num2: number) => num1 / num2,
} as const;

const calc = (operator: string): number => {
    // 出栈
    const num1 = stack.pop();
    const num2 = stack.pop();

    if (typeof num1 !== 'number' || typeof num2 !== 'number') {
        throw new Error('Wrong expression');
    }

    /** 看操作符是不是符合要求的 */
    if (operator in calcMap) {
        return calcMap[operator](Number(num2), Number(num1));
    }

    throw new Error('Unknown expression');
}

中缀表达式转后缀表达式

我们要设计一个计算器程序，用户输入的是更符合人类逻辑思维的中缀表达式，那如何把一个中缀表达式转成后缀表达式呢？

思路

1. 初始化两个栈，operatorStack 用于存储运算符，calcResultStack 用于存储中间运算结果；
2. 从左至右扫描中缀表达式；
3. 遇到操作数时，将其压入 calcResultStack；
4. 遇到运算符时，比较它与 operatorStack 栈顶运算符的优先级：
   1. 如果 operatorStack 为空，或者栈顶运算符为左括号，则直接将它入栈；
   2. 否则，若优先级比栈顶的运算符高，也将其压入 operatorStack；
   3. 否则，将 operatorStack 栈顶的运算符弹出并压入 calcResultStack 中，再把当前的运算符压入到 operatorStack 中；
5. 遇到括号时：
   1. 如果是左括号，则直接压入 operatorStack；
   2. 如果是右括号，则依次弹出 operatorStack 栈顶的运算符，并压入 calcResultStack，直到遇到左括号为止，此时将这一对括号丢弃；
6. 重复步骤 2~5，直到表达式遍历完成，最后把 operatorStack 中还剩余的操作符都放入 calcResultStack 中；

---

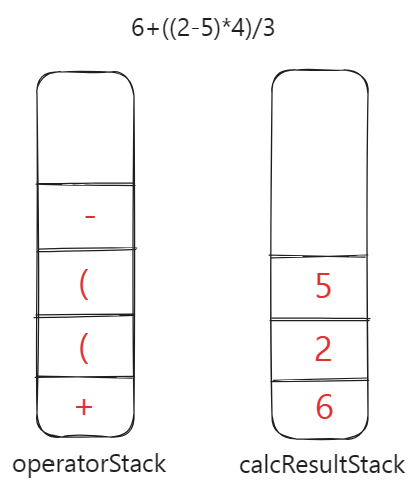
以中缀表达式 6+((2-5)*4)/3 为例（后面以变量exp替代），说明一下步骤。

1. 首先第一步，从左往右遍历表达式，遍历到第一个右括号之前都是入栈的操作。

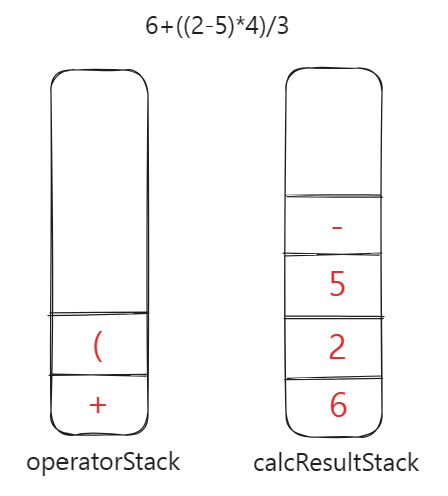
2. 遇到第一个右括号，则依次弹出 operatorStack 栈顶的运算符，并压入 calcResultStack 中，直到遇到第一个左括号未知，并把这个左括号从栈中弹出丢弃。

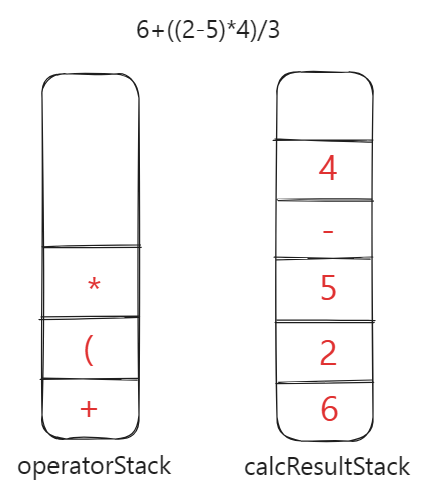
3. 接下来还是继续遍历，依次入栈。

4. 遇到第二个右括号，重复上面的步骤二。

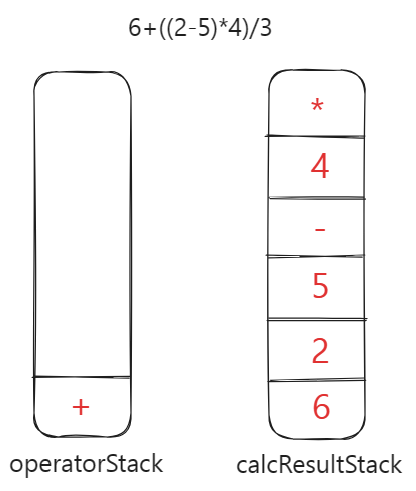
5. 遇到 /运算符，它与 operatorStack 中的栈顶运算符比较，发现优先级比 + 高，则把 / 压入 operatorStack。然后数字 3 压入到 calcResultStack 中。

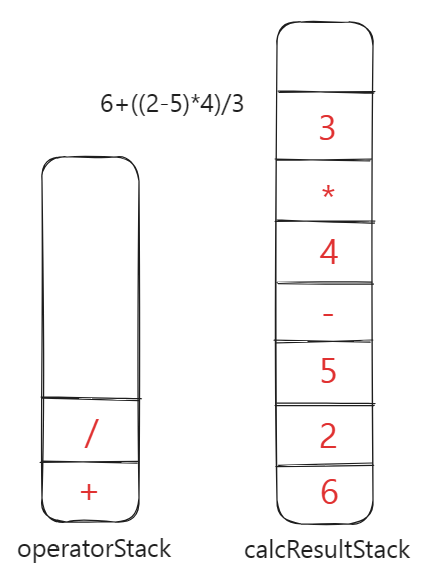
6. 表达式扫描完成，把 operatorStack 中剩余的操作符压入 calcResultStack。

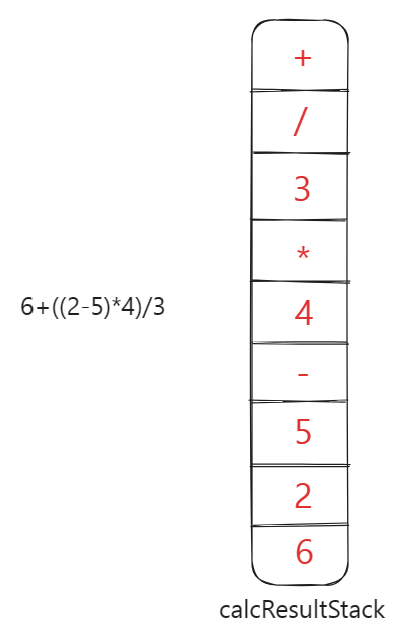
7. 从栈底遍历，得到最终的后缀表达式：625-4*3/+。

实现

首先是一些工具函数，主要包括：

• 存放运算符和中间计算结果的栈；
• 计算函数，用于计算中间值；
• 操作符优先级，用 map 表示；
• 判断字符是不是运算符、数字、括号、小数点等；
• 判断栈顶元素与新传入的操作符谁的优先级高；
• 判断栈顶元素是不是左括号，扫描表达式遇到右括号时会用到；
• 更新栈顶元素，主要是处理操作数时小数或者多于1位的数字；

class Calculator {
    /**
     * 用于存储运算符（+、-、*、/ 等）
     */
    private operatorStack: string[] = [];

    /**
     * 用于存储计算时的中间结果
     */
    private calcResultStack: (number | string)[] = [];

    /** 空格 */
    private spaceReg = /\s+/;

    /**
     * 运算符和优先级，数值越大，优先级越高
     */
    private operator = new Map([
        ['+', 1],
        ['-', 1],
        ['*', 2],
        ['/', 2],
    ]);

    /**
     * 计算函数
     */
    public calcFn = {
        '+': (num1: number, num2: number) => num1 + num2,
        '-': (num1: number, num2: number) => num1 - num2,
        '*': (num1: number, num2: number) => num1 * num2,
        '/': (num1: number, num2: number) => num1 / num2,
    } as const;

    /**
     * 判断传入的字符是不是数字
     * 
     * @param char string
     * @returns boolean
     */
    public isNumber(char: string) {
        const charCode = char.charCodeAt(0);
        return charCode > 47 && charCode < 58;
    }

    /**
     * 判断字符是不是运算符
     */
    public isOperator(char: string) {
        return this.operator.has(char);
    }

    /**
     * 判断字符是不是小数点
     */
    public isPoint(char: string) {
        return char === '.';
    }

    /**
     * 判断是不是左括号
     */
    public isLeftBracket(char: string) {
        return char === '(';
    }

    /**
     * 判断是不是右括号
     */
    public isRightBracket(char: string) {
        return char === ')';
    }

    /**
     * 判断是不是空栈
     */
    public isEmptyStack(stack: string[]) {
        return stack.length <= 0;
    }

    /**
     * 获取栈顶元素
     */
    public getStackTopItem(stack: string[]) {
        return stack[stack.length - 1];
    }

    /** 栈顶元素是不是左括号 */
    public stackTopIsLeftBracket(stack: string[]) {
        var item = this.getStackTopItem(stack);
        return this.isLeftBracket(item);
    }

    /**
     * 判断传入的 operator 是不是比 stack 顶部优先级高
     * 
     * @param stack 操作符栈
     * @param operator 操作符
     * @returns boolean
     */
    public isHigherPriority(stack: string[], operator: string) {
        var top = this.getStackTopItem(stack);
        return this.getPriority(top) < this.getPriority(operator);
    }

    /**
     * 更新数值栈的栈顶
     * 比如遇到小数点，需要把之前的数字拼接上小数点
     * 
     * @param stack 更新数值栈顶
     * @param operator string
     */
    private updateStackTop(stack: (string | number)[], operator: string) {
        let top = stack.pop() ?? "";
        top += operator;
        stack.push(top);
    }

    /**
     * 获取运算符优先级
     * 
     * @param operator 运算符
     * @returns number
     */
    public getPriority(operator: string) {
        return this.operator.get(operator) || -1;
    }

    /**
     * 计算
     */
    private getCalcRes(stack: number[], operator: string) {
        const top = stack.pop();
        const second = stack.pop();
        return this.getResult(second, top, operator);
    }

    /**
     * 计算结果
     */
    public getResult(num1: number, num2: number, operator: string): number {
        if (operator in this.calcFn) {
            return this.calcFn[operator](num1, num2);
        }

        this.throwErr(`Wrong expression', ${num1} ${operator} ${num2}`);
    }

    /** 异常 */
    private throwErr(error: any = 'Wrong expression'): never {
        throw new Error(error);
    }
}

转换函数

转换函数内部会遍历中缀表达式，遇到一个字符就需要判断是操作符还是数字或者别的类型，然后做相应的处理。

public transform(expression: string): (string | number)[] {
    let prevVal = '';   // 记录前一个字符
    const { operatorStack, calcResultStack } = this;

    for (let item of expression) {
        // 当是空格时，则忽略
        if (this.spaceReg.test(item)) continue;

        // 是数字
        if (this.isNumber(item)) {
            // TODO...
        }

        // 是小数点
        else if (this.isPoint(item)) {
            // TODO...
        }

        // 是操作符
        else if (this.isOperator(item)) {
            // TODO...
        }
        

        // 是左括号，直接 push
        else if (this.isLeftBracket(item)) {
            operatorStack.push(item);
        }

        // 是右括号
        else if (this.isRightBracket(item)) {
            // TODO...
        }

        // 否则认为表达式不正确
        else {
            return this.throwErr();
        }

        // 更新前一个值
        prevVal = item;
    }

    // 最后把剩下的操作符移入 calcResultStack 中
    while(operatorStack.length) {
        calcResultStack.push(operatorStack.pop());
    }

    return calcResultStack;
}

上面代码中除了左括号和空格时好处理，其他都需要额外的边界判断，下面一一分析。

首先是数字时，代码如下：

// 是数字
if (this.isNumber(item)) {
    // 如果当前是数字，看看上一次的输入是不是也是数字或者小数点，
    // 是的话就拼接，否则就直接 push
    prevVal && (this.isNumber(prevVal) || this.isPoint(prevVal)) ?
        this.updateStackTop(calcResultStack, item) :
        calcResultStack.push(Number(item));
}

然后是小数点：

// 是小数点
else if (this.isPoint(item)) {
    // 如果当前是小数点，prevVal 是数字，那么就检查栈顶元素是不是已经有了小数点
    const top = this.getStackTopItem(calcResultStack);
    // 栈顶和当前都是小数点，认为表达式不正确
    if (top === '.')    return this.throwErr();
    // 没有小数点就更新栈顶元素（字符拼接）
    this.updateStackTop(calcResultStack, item);
}

然后是操作符：

// 是操作符
else if (this.isOperator(item)) {
    // 当前和上一次都是操作符，则认为表达式不正确
    if (prevVal && this.isOperator(prevVal)) {
        return this.throwErr();
    }

    while (true) {
        // 如果操作符栈是空栈，或者栈顶是左括号，则直接 push
        if (this.isEmptyStack(operatorStack) || this.stackTopIsLeftBracket(operatorStack)) {
            operatorStack.push(item);
            break;
        }

        // 如果栈顶运算符比当前的运算符优先级低，则直接 push
        if (this.isHigherPriority(operatorStack, item)) {
            operatorStack.push(item);
            break;
        }

        // 否则，把栈顶元素弹出，然后加入到 calcResultStack
        // 循环直到 operatorStack 变成空栈或者顶运算符比 item 优先级高
        const top = operatorStack.pop();
        calcResultStack.push(top);
    }
}

最后是右括号：

// 是右括号，需要弹出 operatorStack 中的操作符
// 直到遇到第一个左括号结束
else if (this.isRightBracket(item)) {
    let hasLeftBracket = false;

    while (operatorStack.length) {
        // 弹出操作符栈栈顶元素
        const op = operatorStack.pop();
        // 判断是不是左括号，是的话跳出循环
        if (this.isLeftBracket(op)) {
            hasLeftBracket = true;
            break;
        }
        // 不是左括号，则把运算符 push 到 calcResultStack
        calcResultStack.push(op);
    }

    // 到最后都没有找到左括号，说明表达式有问题
    if (!hasLeftBracket) return this.throwErr();
}

transform 函数最后返回的是一个 Array<number|string>，内部可能是操作符、小数数字或者整数。

计算函数

转换成逆波兰式后，接下来就是最终的计算了，代码与上面 逆波兰式求值过程 章节基本一样，代码如下：

public calc(expression: (string | number)[]) {
    const stack: number[] = [];

    for (let item of expression) {
        // 是数字，并且不是 NaN
        if (typeof item === 'number' && item === item) {
            stack.push(item);
        }

        // 是字符串类型
        else if (typeof item === 'string') {
            // 是空白字符，则忽略
            if (this.spaceReg.test(item)) continue;
        
            const num = Number(item);
            // 是数字字符，直接 push
            if (num === num) {
                stack.push(num);
                continue;
            }
        
            // 是操作符
            else if (this.isOperator(item)) {
                if (stack.length > 1) {
                    const newVal = this.getCalcRes(stack, item);
                    stack.push(newVal);
                }

                // 如果 stack 中没有两个数值，表明这个表达式不合法
                else return this.throwErr();
            }
        } else {
            return this.throwErr();
        }
    }

    // 返回最终结果
    return stack[0];
}

到此，一个简单的计算器就实现了，简单测试一把：

// test-1: 支持小数
let exp = '1.8+((2-3.5)*4)-5.8';
let calcu = new Calculator();
let rs = calcu.transform(exp);
console.log('rs-1 ===>', rs);
console.log('result-1 ===>', calcu.calc(rs));    // -10

// test-2
exp = '6*((13-5)/4)+3';
calcu = new Calculator();
rs = calcu.transform(exp);

console.log('rs-2 ===>', rs);
console.log('result-2 ===>', calcu.calc(rs));    // 15

前缀表达式

除了中缀表达式和后缀表达式外，还有前缀表达式，前缀表达式的操作符通常都在数字的前面。

前缀表达式求值过程如下：

1. 从右至左遍历前缀表达式；
2. 遇到数字压入堆栈；
3. 遇到运算符时，弹出栈顶两个数，用运算符做相应的运算（栈顶元素和次顶元素），并将结果入栈；
4. 重复上面操作过程，直到遍历完表达式；

比如 (3+4)*5-6 对应的前缀表达式为 -*+3456，求值过程就不演示了，大家可以按照上面步骤演算一下。